Билијар
| време | меморија | улаз | излаз |
|---|---|---|---|
| 0,1 s | 64 Mb | стандардни излаз | стандардни улаз |
Билијарски сто је правоугаоног облика димензије \(m\times n\) и има четири рупе у ћошковима. Лоптица се удара из поља са целобројним координатама \((x, y)\) (при чему то не може бити нека рупа), дуж линије која је паралелна или је под углом од 45 степени у односу на неку од ивица стола. Ако претпоставимо да лоптица не успорава своје кретање, да се од сваке се ивице одбија под углом од \(45^\circ\), да је веома мала и да у рупу упада само ако су јој координате центра једнаке координати рупе, напиши програм који одређује да ли ће лоптица некада упасти у рупу и ако хоће у коју рупу ће упасти.
Улаз
Са стандардног улаза се учитава 6 целих бројева. Димензије стола \(m\) и \(n\) (\(1 \leq m, n \leq 10^9\)), координате почетне позиције лоптице \(x\) и \(y\) (\(0\leq x \leq m\) и \(0 \leq y \leq n\)), тако да те координате не одређују рупу и хоризонтална и вертикална компонента брзине лоптице \(v_x\) и \(v_y\) (\(-1 \leq v_x, v_y \leq 1\)).
Излаз
На стандардни излаз исписати координате рупе у коју ће упасти лоптица или \(-1\) ако ће се лоптица бесконачно дуго одбијати.
Пример 1
Улаз
4 3 2 2 -1 1
Излаз
0 0
Објашњење
Путања лоптице је приказана на слици.
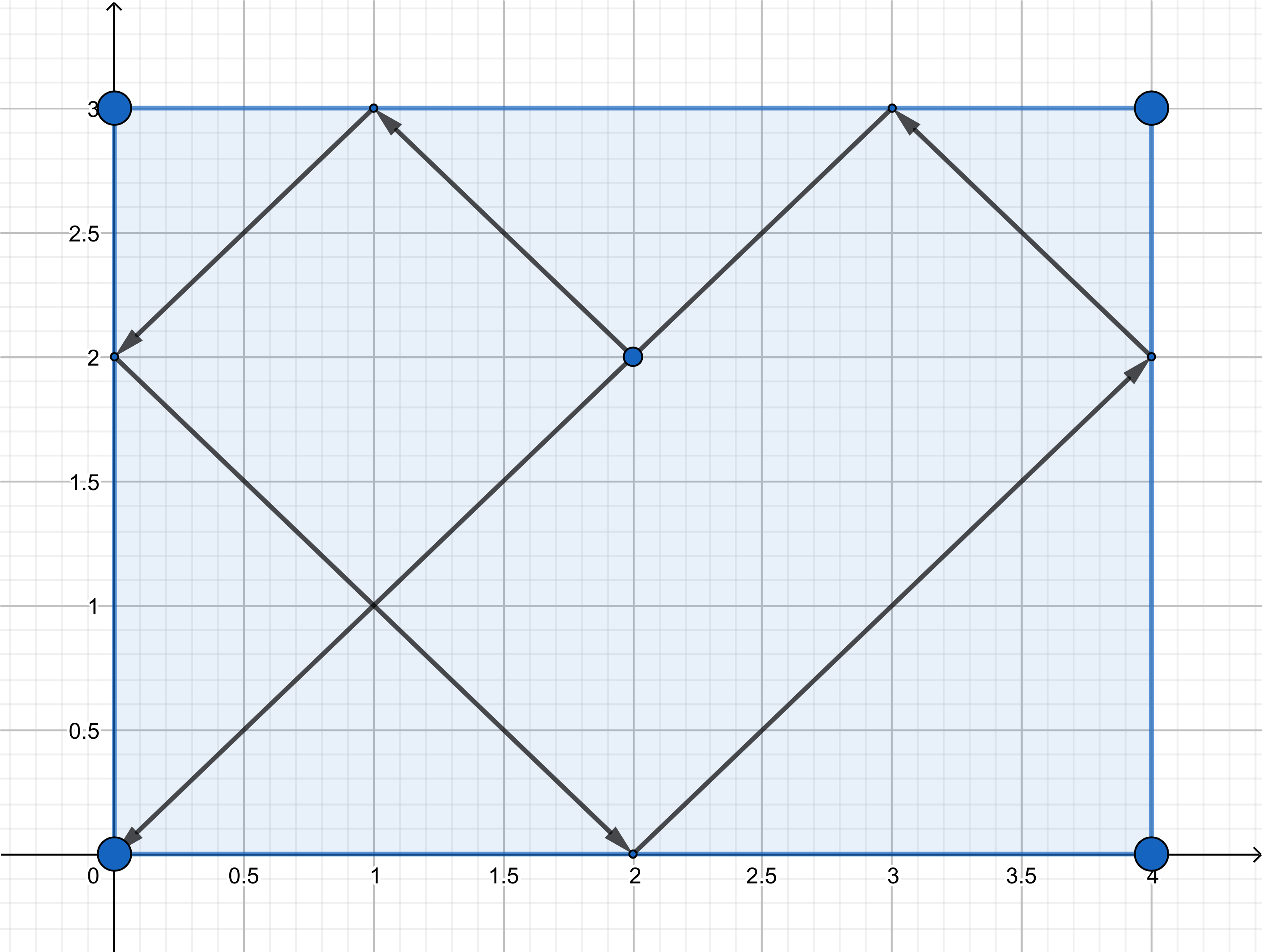
Пример 2
Улаз
4 4 2 0 1 1
Излаз
-1
Пример 3
Улаз
10 10 10 1 -1 0
Излаз
-1
Морате бити улоговани како бисте послали задатак на евалуацију.
